Question

Sam invests $2,000 in an account with an interest rate of 6.7% compounded annually for 3 years.What is the return on investment for Sam's account?

Answer 1

Given:

Principal = $2000

Interest rate = 6.7% compounded annually.

Time, t = 3 years

Let's find the return on investment for Sam's account.

Since it is compounded annually, let's apply the compound interest formula:

`A=P(1+r)^t`

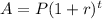
Where:

A is the final amount after 3 years

P is the principal = $2000

r is the interest rate = 6.7% = 0.067

t is the time = 3

Thus, we have:

`\begin{gathered} A=2000(1+0.67)^3 \\ \\ A=2000(1.067)^3 \\ \\ A=2000(1.214767763) \\ \\ A=2429.54 \end{gathered}`

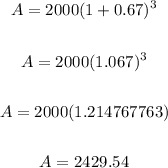
The final amount that will be in Sam's account after 3 years is $2,429.54

To find the ROI, apply the formula:

`ROI=\frac{\text{ final amount - principal}}{principal}*100`

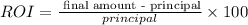
Thus, we have:

`\begin{gathered} \text{ROI}=(2429.54-2000)/(2000)*100 \\ \\ \text{ROI}=(429.54)/(2000)*100 \\ \\ \text{ROI}=21.5\text{ \%} \end{gathered}`

Therefore, the return on investment for Sam's account is 21.5%

ANSWER:

21.5%