Given:
Two points are (-1,10) and (-5,3).
Required:
Find the distance between the given points.
Step-by-step explanation:
The distance between two points is given by the formula:
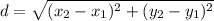
consider
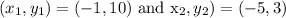
The distance between the given points is:
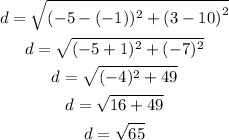
Final Answer:
The distance between the given points is
