the arc length of AB is 8
Step-by-step explanation
the length of arc is given by:
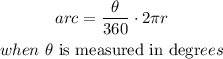
and the circumference of a circle is given by
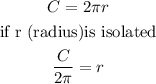
so
Step 1
find the radius of the circle

Step 2
Now, let's find the arc length
let
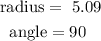
now, let's replace in teh formula for the arc length

therefore, the arc length of AB is 8
I hope this helps you