Question

Solve the following system of equations using an inverse matrix. You must alsoindicate the inverse matrix, A-1, that was used to solve the system. You mayoptionally write the inverse matrix with a scalar coefficient.-2x-y = -56x+y = 9

Answer 1

Given the system of equations:

`\begin{gathered} -2x-y=-5 \\ 6x+y=9 \end{gathered}`

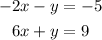
Write the inequalities in matrix form.

`\begin{bmatrix}{-2} & {-1} \\ {6} & {1}\end{bmatrix}\begin{bmatrix}{x} & {} \\ {y} & \end{bmatrix}=\begin{bmatrix}{-5} & {} \\ {9} & \end{bmatrix}`

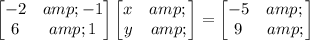
It is of the form Ax = b, where

`A=\begin{bmatrix}{-2} & {-1} \\ {6} & {1}\end{bmatrix},b=\begin{bmatrix}{-5} & {} \\ {9} & {}\end{bmatrix}`

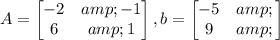
Find the inverse of A.

If

`A=\begin{bmatrix}{a} & {b} \\ {c} & {d}\end{bmatrix}`

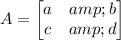
is an invertibe square matrix, then its inverse is

`A=(1)/(\det A)\begin{bmatrix}{d} & {-b} \\ {-c} & {a}\end{bmatrix}`

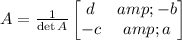
Thus, the inverse of the matrix A is

`A^(-1)=(1)/(4)\begin{bmatrix}{1} & {1} \\ {-6} & {-2}\end{bmatrix}`

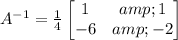
The solution of the system of equations is

`\begin{gathered} (1)/(4)\begin{bmatrix}{1} & {1} \\ {-6} & {-2}\end{bmatrix}\begin{bmatrix}{-5} & {} \\ {9} & {}\end{bmatrix}=(1)/(4)\begin{bmatrix}{4} & {} \\ {12} & {}\end{bmatrix} \\ =\begin{bmatrix}{1} & {} \\ {3} & {}\end{bmatrix} \end{gathered}`

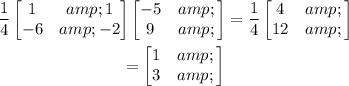
implies that x = 1, y = 3.