Given:
(10, -3), (6, 7) and (9,-5)
To determine the perimeter of the triangle based on the given vertices, we first draw the triangle as shown below :
Next, we use the distance formula:
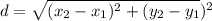
To get the distance from A to B, we let:
We plug in what we know:
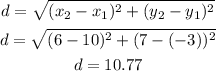
To get the distance from A to C, we let:
So,
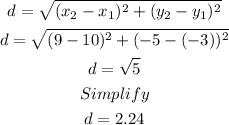
To get the distance from B to C, we let:
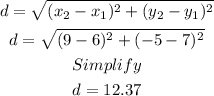
Hence, the perimeter of the triangle:
Perimeter = 10.77+2.24+12.37=25.38
Therefore, the answer is 25.38.