Question

rogers rent video games. a person that purchase a $2 membership can rent games for $0.50 each, if a person wishes to rent games without a membership they are charged $0.75 per gamea) Write the equations for renting gamesb) graph the equations and determine the intersection point

Answer 1

We have that if a person purchases the $2 dollar membership, then the rate of renting the games is $0.5 for each game. Then, if 'x' is the number of games rented and 'y' is the total cost for renting games, the equation for renting games with membership is:

`y_m=0.5x+2_{}`

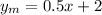
then, for the case where a person rent games without a membership, we have the following equation:

`y_w=0.75x`

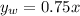
Now, we can graph the equations by using the values y=0 and x=0 to get to points, and then draw the line that goes through them. Then, we have the following for the first equation:

`\begin{gathered} y_m=0.5x+2 \\ x=0\Rightarrow y_m=0.5(0)+2=2 \\ \Rightarrow(0,2)_{} \\ y_m=0\Rightarrow0=0.5x+2\Rightarrow=-(2)/(0.5)=-4 \\ \Rightarrow(-4,0) \\ \\ \end{gathered}`

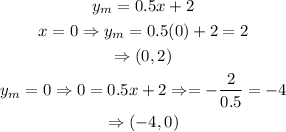
for the second equation we have to make x=4 and y = 0 to get the following points:

`\begin{gathered} y_w=0.75x \\ x=4\Rightarrow y_w=0.75(4)=3 \\ \Rightarrow(4,3) \\ y=0\Rightarrow0.75x=0\Rightarrow x=0 \\ \Rightarrow(0,0) \end{gathered}`

then we have the following lines:

notice that the lines have the intersection point (8,6)