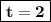Question

Quadrilateral FGHI is a rhombus and mZGFJ = 2t + 59°. What is the value of t?

H
G
t
Submit
J
F
27⁰

Answer 1

t = 2

Explanation:

Rhombus:

ΔGFI is isosceles triangle. GF = FI.

∠FGJ = ∠FIJ

∠FGJ = 27°

In ΔGFJ,

In Rhombus diagonals bisect each other at 90°.

∠GJF = 90°

27° + 90°+ ∠GFJ = 180 {Angle sum property of triangle}

117 + 2t +59 = 180

2t + 176 = 180

2t = 180 - 176

2t = 4

t = 4 ÷ 2

`\sf \boxed{\bf t = 2}`