Question

Kim performed a transformation on rectangle ABCD to create rectangle A'B'C'D', as shown in the figure below:Rectangles ABCD and A prime B prime C prime and D prime are shown. A is at negative 1, 2. B is at negative 1, 5. C is at negative 3, 5. D is at negative 3, 2. A prime is at negative 2, negative 1. B prime is at negative 5, negative 1. C prime is at negative 5, negative 3. D prime is at negative 2, negative 3.What transformation did Kim perform to create rectangle A'B'C'D'? Rotation of 270 degrees counterclockwise about the origin Reflection across the line of symmetry of the figure Reflection across the y‐axis Rotation of 90 degrees counterclockwise about the origin

Answer 1

To determine which transformation we are doing we first need to have the original points of the rectangle, for the original rectangle we have:

`\begin{gathered} A(-1,2) \\ B(-1,5) \\ C(-3,5) \\ D(-3,2) \end{gathered}`

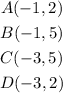
Now, we have to remember that a rotation of 90° counterclockwise about the origin is given by:

`(x,y)\rightarrow(-y,x)`

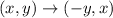
Applying this transformation to the points we have that:

`\begin{gathered} A(-1,2)\rightarrow A^(\prime)(-2,-1) \\ B(-1,5)\rightarrow B(-5,-1) \\ C(-3,5)\rightarrow C^(\prime)(-5,-3) \\ D(-3,2)\rightarrow D^(\prime)(-2,-3) \end{gathered}`

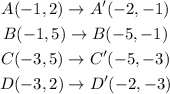
we notice that after the transformation we get the vertexes for the second figure.

Therefore we conclude that the transformation shown is a Rotation of 90 degrees counterclockwise about the origin.