Question

Consider the infinite geometric series (SEE IMAGE) In this image, the lower limit of the summation notation is "n = 1". a. Write the first four terms of the series. b. Does the series diverge or converge? c. If the series has a sum, find the sum.

Answer 1

we have the series

`\sum ^(\infty)_(n\mathop=1)-4((1)/(3))^((n-1))`

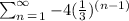
Part a

Write the first four terms of the series.

First-term

For n=1

substitute

`\begin{gathered} \sum ^(\infty)_{n\mathop{=}1}-4((1)/(3))^((1-1)) \\ \sum ^(\infty)_{n\mathop{=}1}-4((1)/(3))^0=-4 \end{gathered}`

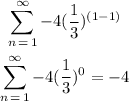
Second term

For n=2

`\sum ^(\infty)_{n\mathop{=}1}(-4)-4((1)/(3))^((2-1))=-4-(4)/(3)=-(16)/(3)`

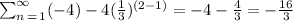
Third term

For n=3

`\sum ^(\infty)_{n\mathop{=}1}-(16)/(3)-4((1)/(3))^((3-1))=-(16)/(3)-(4)/(9)=-(52)/(9)`

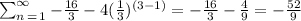
Fourth term

For n=4

`\sum ^(\infty)_{n\mathop{=}1}-(52)/(9)-4((1)/(3))^((4-1))=-(52)/(9)-(4)/(27)=-(160)/(27)`

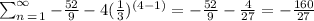
therefore

the first four terms of the series are

-4,-16/3,-52/9,-160/27

Part B

Does the series diverge or converge?

Remember that

if −1In this problem

the common ratio r is equal to 1/3

so

r< 1

that means

The series converges

Part C

If the series has a sum, find the sum

In this problem

the series converges, and it has a sum.

the sum is equal to -6