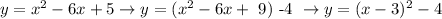Question

Given the picture, what is the equation on the graph?y = - (x + 3) ^ 2 - 4y = (x + 3) ^ 2 -4y = - (x - 3) ^ 2 -4y = (x - 3) ^ 2 - 4

Answer 1

First, lets remenber some properties of de second degree polynomial.

Given a polynomial with the form:

`y=ax^2+bx+c`

We can factor it as:

`y=a(x-r_1)(x-r_2)`

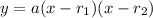
where r_1 and r_2 are the roots of the polynomial.

Also, the polynomial "cuts" the Y axi in 'c', as follows:

`y=a(0)^2+b(0)+c=c`

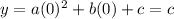
Or, in other words, in the point (0,c).

With those informations, we can solve our question.

From the graph, we can see that the roots are 1 and 5.

So, our polynomial would have the form (in the factored form):

`y=a(x-1)(x-5)`

Expanding our expression, we have:

`y=a(x-1)(x-5)\rightarrow y=ax^2-6ax+5a`

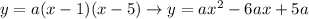
So, in our expression, c=5a. From the graph, we can see that the parabola cuts the Y in the point (0,5), so 'c' must be equal to 5. With that we can find the value of a, as follows:

`c=5\rightarrow5a=5\rightarrow a=1`

So, our polynimial has the form:

`y=x^2-6x+5\rightarrow y=(x^2-6x+\text{ 9) -4 }\rightarrow y=(x-3)^2-4`