Question

Graph the inequality on the axes below.2x + 3y < 15

Answer 1

Explanation:

Given information

2x + 3y < 15

To graph the above inequality, we need to find the x-intercept and the y-intercept

To find the x-intercept and y-intercept, we need to express the inequality in terms of an equation. Therefore, we have the below equation

2x + 3y = 15

To find x-intercept, isolate y by making it zero

hence, y = 0

`\begin{gathered} 2x\text{ + 3(0) = 15} \\ 2x\text{ + 0 = 15} \\ 2x\text{ = 15} \\ \text{Divide both sides by 2} \\ \frac{\cancel{2}x}{\cancel{2}}\text{ = }(15)/(2) \\ x\text{ = }(15)/(2) \end{gathered}`

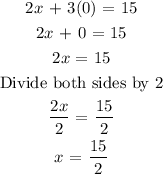
The x-intercept is (15/2, 0)

To find y-intercept, make x = 0

`\begin{gathered} 2(0)\text{ + 3y = 15} \\ 0\text{ + 3y = 15} \\ 3y\text{ = 15} \\ \text{Divide both sides by 3} \\ \frac{\cancel{3}y}{\cancel{3}}\text{ = }\frac{\cancel{15}\text{ 5}}{\cancel{3}} \\ y\text{ = 3} \end{gathered}`

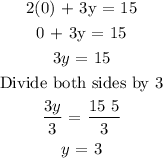
The y-intercept is (0, 3)

The next step is to plot the calculated coordinate points

(15/2, 0) and (0, 3)