Question

How long does it take the perdón to get to the top?

Answer 1

Since the escalator is 20 meters long and it takes 50 seconds to ride from the bottom to the top, the escalator speed is given by:

`\text{speed}=\frac{\text{distance}}{\text{time}}=(20)/(50)=0.4\text{ m/s}`

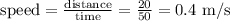
Since the person starts walking with a speed of 1 m/s, then the relative speed is the sum of the person speed and the escalator speed:

`\text{speed}=0.4+1=1.4\text{ m/s}`

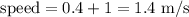
So, calculating the time for a distance of 20 meters, we have:

`\begin{gathered} \text{distance}=\text{speed}\cdot\text{time} \\ 20=1.4\cdot t \\ t=(20)/(1.4)=14.286\text{ seconds} \end{gathered}`

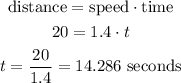
It takes 14.286 seconds for a person to get to the top.

Now, to calculate the force needed, let's first calculate the acceleration, then we use the second law of Newton to calculate the force:

`\begin{gathered} a=(\Delta V)/(\Delta t)=(1)/(0.6)=1.667 \\ \\ F=m\cdot a=60\cdot1.667=100\text{ N} \end{gathered}`

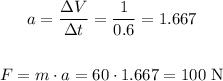
The force needed is 100 N.

If the escalator angle is 15° and its length is 20 meters, we can calculate the height with the formula for the vertical component:

`\begin{gathered} h=\text{length}\cdot\sin (15\degree) \\ h=20\cdot0.2588 \\ h=5.176\text{ meters} \end{gathered}`

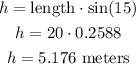
The height lifted is 5.176 meters.

The potential energy (PE) can be calculated with the formula below:

`\begin{gathered} PE=m\cdot g\cdot h \\ PE=60\cdot9.8\cdot5.176 \\ PE=3043.488\text{ J} \end{gathered}`

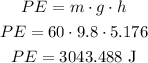
The potential energy (PE) is 3043.488 J.