To find the Length of MKL, we need to find the length of JM and JL using the length of an arc formula
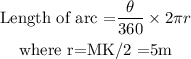
STEP 1
Find the angle subtended at N and find the arc JM
N +52= 180 -------sum of angles on a straight line.
N= 180-52
N=128
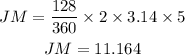
STEP 2
Find the length of JL
The angle subtended at Therefore,
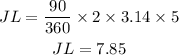
STEP 3
Find the lenght of MKL. MKL is the sum of JM and JL
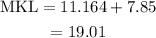
The answer is 19.01m