Question

If MK = 10 m, find the length of MKL.K52LMMRound the answer to 2 decimal places.meters

Answer 1

To find the Length of MKL, we need to find the length of JM and JL using the length of an arc formula

`\begin{gathered} \text{Length of arc =}(\theta)/(360)*2\pi r \\ \text{where r=MK/2 =5m} \end{gathered}`

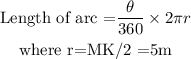
STEP 1

Find the angle subtended at N and find the arc JM

N +52= 180 -------sum of angles on a straight line.

N= 180-52

N=128

`\begin{gathered} JM=(128)/(360)*2*3.14*5 \\ JM=11.164 \end{gathered}`

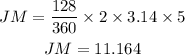
STEP 2

Find the length of JL

The angle subtended at Therefore,

`\begin{gathered} JL=(90)/(360)*2*3.14*5 \\ JL=7.85 \end{gathered}`

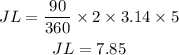
STEP 3

Find the lenght of MKL. MKL is the sum of JM and JL

`\begin{gathered} \text{MKL}=11.164+7.85 \\ =19.01 \end{gathered}`

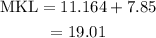
The answer is 19.01m