ANSWER:
x = 4.5
Step-by-step explanation:
Since Q bisects PR, it means that Q divides the line PR exactly by half.
This means PQ = QR
Given:
PR = 28
PQ = 2x + 5
To find x, we have:
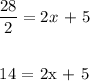
Solve for x:
Subtract 5 from both sides:

Divide both sides by 2:
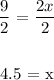
x = 4.5