We are given that a bullet initially at rest has a final velocity of 100 m/s after accelerating in a barrel that is 1.000 meters long. To determine the acceleration we will use the following equation of motion:
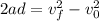
Where:

Since the bullet starts at rest this means that the initial velocity is zero, therefore:
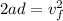
Now, we solve for the acceleration by dividing both sides by "2d"
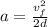
Plugging in the values:
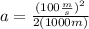
Solving the operations:

Part B. We are asked to determine the time that it takes the bullet to travel the distance. To do that we will use the following formula:
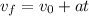
Now, we solve for the time "t". First, we set the initial velocity to zero;
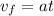
Now, we divide both sides by the acceleration:
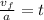
Now, we plug in the values:
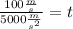
Now, we solve the operations:

Therefore, the time is 0.02 seconds.