Let x be the width of the matting, since it is of equal width and the total area is equal to 10000cm^2 (1m^2=1mx1m=100cmx100cm=10000cm^2); then,
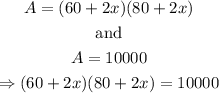
In a diagram
Solving for x,
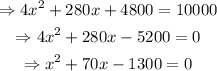
Solving the quadratic equation,
![\Rightarrow x=\frac{-70\pm\sqrt[]{4900+4\cdot1300}}{2}=-35\pm\frac{\sqrt[]{10100}}{2}\Rightarrow-35\pm5\sqrt[]{101}](https://img.qammunity.org/2023/formulas/mathematics/college/78qsbwlexryg0ozgfvwrb8znhvjkly1nr4.png)
And x has to be a positive number since it is a measurement; therefore,
![\begin{gathered} \Rightarrow x=5\sqrt[]{101}-35 \\ \Rightarrow x=15.249378\ldots \\ \Rightarrow x\approx15.25 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ni96flsn2zyra89fe6cd73g1b1dfg5azsi.png)
The answer is approximately 15.25cm.