Answer:
Any 4: 15
At least 4: 22
Step-by-step explanation:
The number of ways to select x elements from a group of n is calculated as
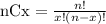
So, the number of ways to select any 4 from a group of 6 is
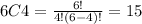
On the other hand, the number of ways to select at least 4 is the sum of the number of ways to select 4, the number of ways to select 5, and the number of ways to select 6.
Since 6C5 and 6C6 is equal to

We get that the number of ways to select at least 4 is equal to
6C4 + 6C5 + 6C6 = 15 + 6 + 1 = 22
Therefore, the answers are:
Any 4: 15
At least 4: 22