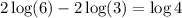Question

Write the expression as a single logarithm. (Simplify your answer.)2log(6)-2log(3)

Answer 1

log 4

Explanation:

Given the logarithm expression:

`2\log (6)-2\log (3)`

To write the expression as a single logarithm, first factor out 2.

`=2\lbrack\log (6)-\log (3)\rbrack`

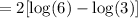
Next, when logarithms in the same base are being subtracted, we can combine it as follows:

`\begin{gathered} \log (A)-\log (B)=\log ((A)/(B))\implies\log (6)-\log (3)=\log ((6)/(3)) \\ \implies2\lbrack\log (6)-\log (3)\rbrack=2\log ((6)/(3))=2\log (2) \end{gathered}`

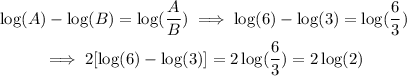
Finally, when a number is multiplying a logarithm expression, we can rewrite it as follows:

`\begin{gathered} x\log y\implies\log y^x \\ \implies2\log (2)=\log 2^2=\log 4 \end{gathered}`

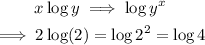
Thus, the expression written as a single logarithm gives the equality:

`2\log (6)-2\log (3)=\log 4`