Question

The half-life of carbon-14 is 5,730 years. Suppose a fossil is found with 15 percent, as much of its carbon-14 as compared to a living simple. How old is the fossil? Round to the nearest year

Answer 1

Hello there. To solve this question, we'll have to remember some properties about half-life of carbon-14.

We can use the following formula to determine how many years has passed by finding how many half-life sessions the carbon-14 endured:

`t=\mleft\lbrack(\ln\mleft((N)/(N_0)\mright))/(-0.693)\mright\rbrack\cdot t_{(1)/(2)}`

In which:

`t_{(1)/(2)}=5730`

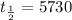
In this case, N is the amount of sample we have after the period t of time and N0 is what we started with.

Knowing that the fossil was found with 15% of its initial sample, this means that the ratio N/N0 = 15/100 = 3/20=0.15

Therefore we have:

Using a calculator, we find that ln(0.15) is approximately equal to -1.89712, thus

Multiply the numbers and round the answer to the nearest year: