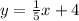Question

Write the slope-intercept form of the equation of the line described.Through (-5,3), perp. to y = -5x -3

Answer 1

We know that two lines are perpendicular if and only if their slopes fullfil:

`m_1m_2=-1`

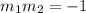
We know that the line we are looking for is perpendicular to the line:

`y=-5x-3`

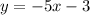
Comparing this line with:

`y=mx+b`

we conclude that the line y=-5x-3, has slope -5.

Now, plugging this values into the condition of perpendicularity we have that:

`\begin{gathered} -5m=-1 \\ m=(-1)/(-5) \\ m=(1)/(5) \end{gathered}`

This means that the line we want has slope 1/5.Now the equation of a line with slope m that passes through the point (x1,y1) is given by:

`y-y_1=m(x-x_1)`

Plugging the slope we found and the point given we have that:

`\begin{gathered} y-3=(1)/(5)(x-(-5)) \\ y-3=(1)/(5)(x+5) \\ y-3=(1)/(5)x+1 \\ y=(1)/(5)x+4 \end{gathered}`

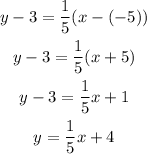
Therefore the line is:

`y=(1)/(5)x+4`