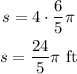Question

Find the length of the arc shown in red. Leave your answer in terms of
`\pi`

Answer 1

The length of the arc (s), the central angle θ, and the radius (r) are related as follows:

`s=r\cdot\theta`

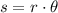
where θ must be in radians

The central angle related to arc length in red is 360°- 144° = 216°

360° are equivalent to 2π radians, then

`\theta=216\text{ \degree}\cdot\frac{2\pi\text{ radians}}{360\text{ \degree}}=(6)/(5)\pi\text{ radians}`

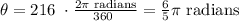
Substituting this value of θ and r = 4 ft, the arc length is:

`\begin{gathered} s=4\cdot(6)/(5)\pi \\ s=(24)/(5)\pi\text{ ft} \end{gathered}`