Question

Victor biked from his hometown to a neighboring city in 6 hours. He biked back to his hometown in 4 hours. His speed on the return trip was 4 mph faster than his speed on the first trip. How far apart are the two cities?

Answer 1

We will have the following:

His speed on the return (r) trio was 4mph faster than his speed in the first trip (o), so:

`r=o+4`

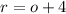
Then, we have that speed times distance equals time, and distance is equal to time over speed. Thus:

`6h(\frac{x}{\text{hours}})=4h(\frac{x+4}{\text{hours}})`

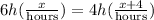
Then, we have:

`6x=4x+16\Rightarrow2x=16`
`\Rightarrow x=8`

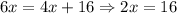
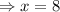
So, the initial speed was of 8mph.

Then we deternine the distance:

`d=(8mi/h)(6h)\Rightarrow d=48mi`

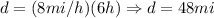
So, the two cities are 48 miles apart.