Question

f(x) =6x-8g(x) =x+8 / 6Find the domains of (f o g) and (g o f) and write your answer in interval notation.

Answer 1

`(-\text{ }\infty,\text{ +}\infty)`

Step-by-step explanation

We have to first find (f o g) and (g o f).

(f o g) means f(g(x)), that is:

`\begin{gathered} f(g(x))\text{ = 6(}\frac{x\text{ + 8}}{6})\text{ - 8} \\ (f\text{ o g)(x) = x + 8 - 8} \\ (f\text{ o g) = x} \end{gathered}`

(g o f) means g(f(x)), that is:

`\begin{gathered} g(f(x))\text{ = }\frac{6x\text{ - 8 + 8}}{6}\text{ = }(6x)/(6) \\ (g\text{ o f) = x} \end{gathered}`

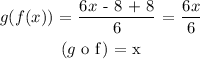
The two functions (since they are identical) do not have any undefined points.

The domain of a function is the set of all the possible values of x.

Therefore, since there are no undefined points in the function, the domain is (-infinity, + infinity)