Question

Drag the tiles to the correct boxes not all tiles will be used

Answer 1

We want to determine the right steps that can be used to solve

`(x^2+7x+10)/(x^2+4x+4).(x^2+3x+2)/(x^2+6x+5)`

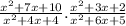
Now the first step will be to factorise each of the quadratic expression This becomes

`\begin{gathered} (x^2+2x+5x+10)/(x^2+2x+2x+4).(x^2+1x+2x+2)/(x^2+5x+1x+5) \\ (x(x+2)+5(x+2))/(x(x+2)+2(x+2)).(x(x+1)+2(x+1))/(x(x+5)+1(x+5)) \\ ((x+2)(x+5))/((x+2)(x+2)).((x+1)(x+2))/((x+5)(x+1)) \end{gathered}`

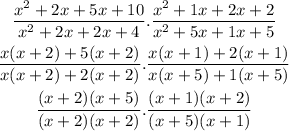
Hence the first step to drag into the tile is

`((x+2)(x+5))/((x+2)(x+2)).((x+1)(x+2))/((x+5)(x+1))`

The next step is to cancel out the common factors. This becomes

`\begin{gathered} ((x+2)(x+5))/((x+2)(x+2)).((x+1)(x+2))/((x+5)(x+1)) \\ \text{Here we cancel out }(x+2)\text{ above and below in the first set and } \\ \text{cancel out }(x+1)\text{ above and below in the second part, we will have} \\ ((x+5))/((x+2)).((x+2))/((x+5)) \end{gathered}`

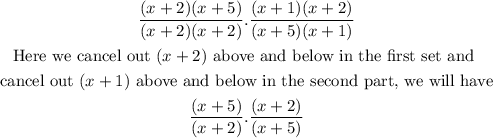
Hence, the second step to drag into the tile is

`((x+5))/((x+2)).((x+2))/((x+5))`

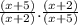
The next step is to multiply by bringing them together, and we have

`\begin{gathered} ((x+5))/((x+2)).((x+2))/((x+5)) \\ =((x+5)(x+2))/((x+2)(x+5)) \end{gathered}`

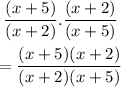
Hence, the third step to drag to the tile is

`((x+5)(x+2))/((x+2)(x+5))`

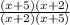
The next step is to cancel out another common factors if there is

`\begin{gathered} ((x+5)(x+2))/((x+2)(x+5)) \\ \text{Here, }(x+5)\text{ is se}en\text{ above and below, we will cancel out to have } \\ ((x+2))/((x+2)) \\ x+2\text{ can cancel out and we will have } \\ 1 \end{gathered}`

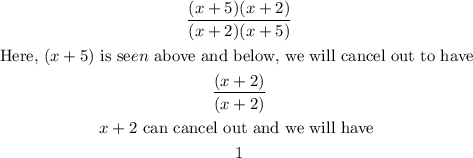
Hence, the final step to drag into the tile is 1