Question

Given the points are they parallel perpendicular skew or none of these

Answer 1

Given points are R(-1,-2), S(5,2), and T(-2,6), U(4,-3)

First find the slope of line RS and TU:

So for RS:

`\begin{gathered} m_(RS)=(2-(-2))/(5-(-1)) \\ m_(RS)=(2+2)/(5+1)=(4)/(6) \\ m_(RS)=(2)/(3) \end{gathered}`

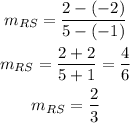
Now the slope of TU:

`\begin{gathered} m_(TU)=(-3-6)/(4-(-2)) \\ m_(TU)=-(9)/(6) \\ m_(TU)=-(3)/(2) \end{gathered}`

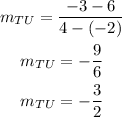
So the condition for both the lines are perpendicular as we know that:

For perpendicular the slope of two lines are:

`m_1=-(1)/(m_2)`

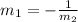
So option B is correct.