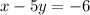Answer:
The equation of the line in standard form is;
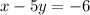
Step-by-step explanation:
Firstly we need to find the slope of each of the lines PQ,QR and PR.
the coordinates of each points are; P(-1,1), Q(3,5) and R(5,-5)
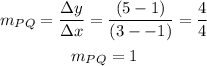
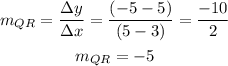
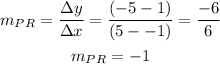
Next we will find the perpendicular lines among PQ,QR and PR.
the product of the slope of perpendicular lines must be equal to -1.
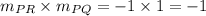
So, line PR and PQ are perpendicular.
The side opposite the perpendicular angle of a right angled triangle is the hypotenuse.
So, the hypotenuse side is the line QR.
Then the line that passes through the perpendicular angle and is perpendiculare to the hypotenuse will have a slope of;

And it will pass through point P(-1,1)
The equation will then be;

Therefore, the equation of the line in standard form is;