Question

1.)A pistol that fires a signal flare gives it an initial velocity (muzzle velocity) of 125m/s at an angle of 55.0 degree above the horizontal.You can ignore air resistance.Find the flare's maximum height and the distance from its firing point to its landing point if it is fired (a) on the level salts flats of Utah, and (b) over the flat Sea of Tranquility on the Moon, where g= 1.67 meter per second squared(m/s2).

Answer 1

This is a projectile motion; we know that the maximum height and the range (the horizontal distance) of a projectile are given as:

`\begin{gathered} h=(v_0^2\sin^2\theta)/(2g) \\ R=(v_0^2\sin2\theta)/(g) \\ \text{ where:} \\ v_0\text{ is the initial velocity of the projectile} \\ \theta\text{ is the angle of launch} \\ g\text{ is the gravitational acceleration} \end{gathered}`

In both situation the initial velocity is 125 m/s and the angle is 55°, with this in mind.

a)

In this case the gravitational acceleration is 9.8 m/s² (we drop the sign in this equations since we only need the magnitude of the accelaration). Plugging the values we have:

`\begin{gathered} h=((125)^2(\sin55)^2)/(2(9.8))=534.93 \\ R=((125)^2\sin(2\cdot55))/(9.8)=1498.23 \end{gathered}`

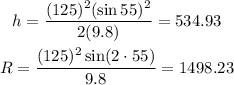
Therefore, the maximum height is 534.93 m and the range is 1498.23 m

b)

In this case the gravitational acceleration is 1.62 m/s² (we drop the sign in this equations since we only need the magnitude of the accelaration). Plugging the values we have:

`\begin{gathered} h=((125)^2(\sin55)^2)/(2(1.62))=3235.97 \\ R=((125)^2\sin(2\cdot55))/(1.62)=9063.39 \end{gathered}`

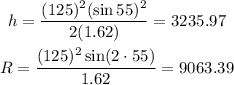
Therefore, the maximum height is 3235.97m and the range is 9063.39 m