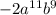Question

Simplify the expression.-10a²b45a-9b-5Write your answer without negative exponents.Enter the correct answer.

Answer 1

`-2a^(11)b^9`

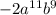
Explanation:

Given the expression:

`(-10a^2b^4)/(5a^(-9)b^(-5))`

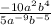
First, rewrite the fraction by separating the constants, and variables a and b.

`\begin{gathered} (-10a^2b^4)/(5a^(-9)b^(-5))=-(10)/(5)*(a^2)/(a^(-9))*(b^4)/(b^(-5)) \\ =-2*(a^2)/(a^(-9))*(b^4)/(b^(-5)) \end{gathered}`

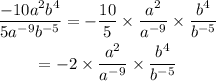
Next, apply the division rule of exponents:

`(x^m)/(x^n)=x^(m-n)`

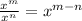
So, we have:

`\begin{gathered} =-2* a^(2-(-9))* b^(4-(-5)) \\ =-2* a^(2+9)* b^(4+5) \\ =-2a^(11)b^9 \end{gathered}`

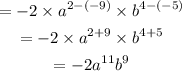
The simplified form of the expression without any negative exponent is:

`-2a^(11)b^9`