Question

Select the correct choice below and, if necessary, fill in any answer boxes within your choice.

Answer 1

A. The solution is x = 4 and y = 1

Explanation:

Given the below system of equations;

`\begin{gathered} x+y=5\ldots\ldots\text{.}\mathrm{}\text{Equation 1} \\ x-y=3\ldots\ldots\text{.}\mathrm{}\text{Equation 2} \end{gathered}`

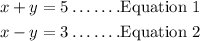
To solve the above system of equations, we'll follow the below steps;

Step 1: Subtract Equation 2 from Equation 1;

`\begin{gathered} (x-x)+(y-(-y))=(5-3) \\ 0+2y=2 \\ y=(2)/(2) \\ y=1 \end{gathered}`

Step 2: Substitute the value of y into Equation 1 and solve for x;

`\begin{gathered} x+1=5 \\ x=5-1 \\ x=4 \end{gathered}`

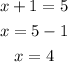
The solution is x = 4 and y = 1

If we convert the given equations into slope-intercept form of the equation of a line generally given as;

`y=mx+b`

where m = slope of the line and b = y-intercept of the line

Converting the two equations, we'll have;

`\begin{gathered} y=-x+5 \\ y=x-3 \end{gathered}`

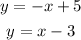
We can see that for the 1st equation, slope(m) = -1 and y-intercept(b) = 5 while for the 2nd equation, slope(m) = 1 and y-intercept(b) = -3.

With the above information, we can go ahead and plot the graphs of both lines as seen below;

We can also see from the graph that, at the point of intersection of both lines, x = 4 and y = 1 which is the solution and it aligns with what we had earlier.