Given:
Total number of asignments, N=5
Average of Syed on 5 assignments, A=91%.
Ms. Crockett has gotten a 91%, 70%, 99%, 81% on the first four assignments.
Let a be the average of Ms. Crockett.
Let x be the grade got by Ms. Crockett on the fifth assignment.
Now, the average of Ms. Crockett can be expressed as,
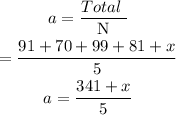
Crockett has to get an average above 91% to beat Ms. Syed.
To find the score x, Ms. Crockett should get in the fifth assignment to beat Syed, put a=91% in the above equation.
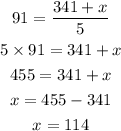
So, Ms. Crockett should get a score greater than 114% to overcome Ms. Syed's average.
But, it is mathematically impossible to get 114%. Hence, Ms. Crockett cannot beat Ms. Syed.