Question

Haley was on a long 223 mile road trip. Tbe first part of the trip there was lots of traffic, she only averages 16 mph. The second part of the trip there was no traffic so she could drive 53 mph. If the trip took her 7 hours, how long did she travel at each speed?

Answer 1

We are given that Haley travels 223 miles, first at a speed of 16 mph and then at a speed of 53 mph if x is the number of hours driving at 16 mph and y the number of hours traveling at 53 mph, this can be expressed mathematically as:

`16x+53y=223,(1)`

We are also told that the total number of hours is 7, this can be represented as:

`x+y=7,(2)`

We get a system of two variables and two equations. To solve the system we will solve for "x" in equation (2) by subtracting "y" to both sides:

`x=7-y`

Replacing the value of "x" in equation (1):

`16(7-y)+53y=223`

Using the distributive property:

`112-16y+53y=223`

Adding like terms:

`112+37y=223`

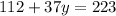
Subtracting 112 to both sides:

`\begin{gathered} 37y=223-112 \\ 37y=111 \end{gathered}`

Dividing by 37 both sides:

`y=(111)/(37)`

Solving the operations:

`y=3`

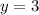
Replacing the value of "y" in equation (2)

`x=7-3=4`

Therefore, she traveled 4 hours at 16 mph and 3 hours at 53 mph