Question

Owen and his friends like to collect and trade cards from a certain combat card game. Owenused his allowance to purchase 1 booster pack and 1 premade deck, which included a total of56 cards. For his birthday, he received 5 booster packs and 1 premade deck, which included atotal of 88 cards. How many cards come in every booster pack and every premade deck?

Answer 1

Answer with Explanation: Let us let B represent a Booster pack and P represent a premade deck, we can write the following simultanous equations:

`\begin{gathered} B+P=56 \\ 5B+1P=88 \end{gathered}`

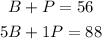
The solution to the system is as follows:

`\begin{gathered} B+P=56 \\ 5B+1P=88 \\ \therefore\rightarrow \\ B=56-p \\ 5(56-P)+1P=88 \\ 280-5P+1P=88 \\ 280-4P=88 \\ 4P=280-88=192 \\ P=(192)/(4)=48 \\ P=48 \\ \therefore\rightarrow \\ B=56-P=56-48=8 \\ B=8 \end{gathered}`

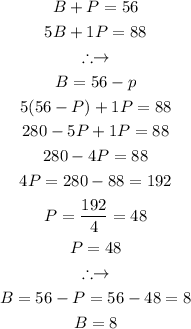
In conclusion, the Booster pack has 8 number of cards and premade deck has 48 number of cards.