Let's begin by listing out the given information
Total number of flowers = 4 + 4 + 8 = 16
Yellow = 4 flowers
Red = 4 flowers
Blue = 8 flowers
The probability that the first flower was red is:
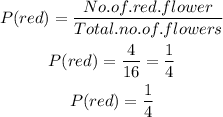
After removing the first flower (red), the probability that the second flower was blue is:
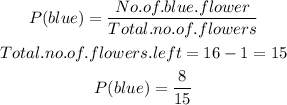
The total probability for this event is given by the product of P(red) & P(blue):
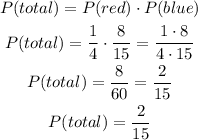
Hence, 2/15 is the answer