A)
Start by graphing the function on the different intervals.
For this, we graph as if they were independent functions and then join them on the same graph.
for x<4
for x>=4
then, for g(x)
B)
To find the x-intercepts:
equal g(x) to 0.
for x<4
![\begin{gathered} x^3-16x=0 \\ x(x^2-16)=0 \\ \text{equal both factors to 0} \\ 1.x=0 \\ 2.x^2-16=0 \\ \text{then,} \\ x^2-16=0 \\ x^2=16 \\ x=\sqrt[]{16} \\ x=\pm4 \\ 4\text{ is not defined on the interval } \\ x-\text{intercepts are 0 and -4} \end{gathered}]()
for x>=4
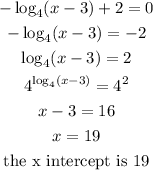
then, for g(x)
For g(x) the x-intercepts are -4, 0 and 19
C)
finally, using the graph we can see that the function is positive in the intervals [-4,0)∪[4,19) because in these intervals g(x) is above the x-axis.