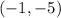By definition:
- Reflection is a transformation in which an object is flipped.
- Dilation is a transformation in which the shape of the object does not change, but its size does.
- The Pre-Image is the object before the transformation and the Image is the object transformated.
- The rule for a reflection over the x-axis is the following:
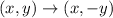
- The rule of a dilation centered at the origin, with the scale factor

is the following:
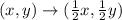
Knowing the above, you can conclude that rule for the transformation given in the exercise, is:
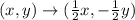
Knowing that the Pre-Image is:
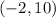
You get that the Image of that point is:
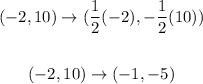
The answer is: