Question

Point X is chosen at random on LP. Find the probability of P(X is on LN).* Please note: LP has a line over it. I don't know how to type that in. Sorry.

Answer 1

The probability is approximately 0.8333 (to 4 decimal places), which is 83.33%.

To find the probability that a point X chosen at random on
`\( \overline{LP} \)` is on
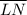`\( \overline{LN} \)`, we need to look at the lengths of
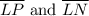`\( \overline{LP} \) and \( \overline{LN} \)` as provided in the image.

Step 1: Calculate the total length of
`\( \overline{LP} \).`

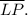
This is found by adding the lengths of
`\( \overline{LM} \)`,
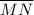`\( \overline{MN} \)`, and
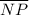`\( \overline{NP} \)` together:

`\[ \overline{LP} = \overline{LM} + \overline{MN} + \overline{NP} \]`

`\[ \overline{LP} = 2 + 8 + 10 + 4 \]`

Step 2: Calculate the length of
`\( \overline{LN} \).`

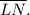
This is found by adding the lengths of
`\( \overline{LM} \)` and
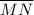`\( \overline{MN} \)` together:

`\[ \overline{LN} = \overline{LM} + \overline{MN} \]`

`\[ \overline{LN} = 2 + 8 \]`

Step 3: Calculate the probability.

The probability
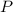`\( P \)` of point X being on
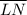`\( \overline{LN} \)` is the ratio of the length of
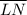`\( \overline{LN} \)` to the length of
`\( \overline{LP} \):`

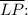
`\[ P(X \text{ is on } \overline{LN}) = \frac{\overline{LN}}{\overline{LP}} \]`

Let's perform these calculations to find the probability.

The total length of
`\( \overline{LP} \)` is 24 units, and the length of
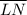`\( \overline{LN} \)` is 20 units.

To find the probability \( P \) of point X being on \( \overline{LN} \):

`\[ P(X \text{ is on } \overline{LN}) = \frac{\overline{LN}}{\overline{LP}} = (20)/(24) \]`

When simplified, the probability is:

`\[ P(X \text{ is on } \overline{LN}) = (5)/(6) \]`

Or in decimal form, the probability is approximately 0.8333 (to 4 decimal places), which is 83.33%.

Answer 2

41.6%

Step-by-step explanation

The probability of an event is the number of favorable outcomes divided by the total number of outcomes possible

Step 1

find the total of out comes possible, it is distance from L to P

distance from L to P=

`\begin{gathered} LM=2 \\ MN=8 \\ NO=10 \\ OP=4 \\ \text{then} \\ LP=2+8+10+4=24 \\ LP=24 \end{gathered}`

Step 2

find the total number of favorable outcomes( X is on LN)

`\begin{gathered} LN=LM+MN \\ \text{replace} \\ LN=2+8 \\ LN=10 \end{gathered}`

Step 3

finally, find the probability

`P=(10)/(24)=0.416`

Hence, the probability is 0.416 or 41.6 %