Question

Solve the system of two linear inequalities waphically{2*5y<10+3yStep 1 of 3 Graph the solution set of the first linear inequalityAnswerКеThe line will be drawn once all required data is provided and will update whenever a value is updated. The regions will be added once the line is drawnEnable Zoom/panChoose the type of boundary lineO Sold) Dashed)Enter two points on the boundary lineSelect the region you wish to be shaded

Answer 1

Step-by-step explanation

The first equation is 2x + 5y < 10. To graph it, we have to find two points that are on the line, so they have to satisfy the equation,

`2x+5y=10`

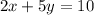
We can use the two intercepts. The x-intercept occurs when y = 0,

`\begin{gathered} 2x+5\cdot0=10 \\ 2x=10 \\ x=(10)/(2)=5 \end{gathered}`

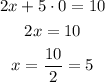
And the y-intercept occurs when x = 0,

`\begin{gathered} 2\cdot0+5y=10 \\ 5y=10 \\ y=(10)/(5)=2 \end{gathered}`

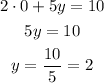
So, the two points we can use are (5, 0) and (0, 2).

Then, to find what type of line we have to use and what area to shade, we have to solve the inequality for y: subtract 2x from both sides, and divide both sides by 5,

`\begin{gathered} 2x-2x+5y<10-2x \\ 5y<10-2x \\ \\ y<2-(2)/(5)x \end{gathered}`

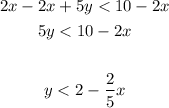
Since y is less than the line, we have to use a dashed line and shade the area below the line,

The second inequality is x ≥ -5. To graph it, we have to draw a vertical continuous line passing through x = -5. Since x is greater than or equal to -5, the area that has to be shaded is the area to the right of the line,

Two points that lie on this line are (-5, -1) and (-5, 1). Any point whose x-coordinate is -5 will be on this line.