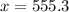We have the next triangle
And we must find the value of x
In order to find the value of x we must use the given angle
So, we need a trigonometric function that relate the opposite and the adjacent legs of the right triangle
We can see that the trigonometric function we need is tan θ
In this case the angle is 78.3°, the opposite is x and the adjacent is 115
Then, replacing the values in the equation for tan θ
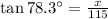
Finally, we must solve the equation for x
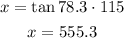
ANSWER: