Directions: Find the area of each figure.(Hint: Round to the nearest tenth.)8 cmBlank 1:I

Question

asked Apr 18, 2023 5.2k views

1 Answer

Awebartisan · Answer 1 · 2023-04-23T23:57:03+0000

Let's suppose that the dashed line bisect the right angle and the figure is a square. Then, we can draw the following picture

then, we can draw the following right triangle

and we need to find x. This can be done as

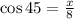
$\cos 45=(x)/(8)$

then x is equal to

$x=8\cos 45$

since cos 45 is

$\cos 45=\frac{1}{\sqrt[]{2}}$

then, x is given by

$x=\frac{8}{\sqrt[]{2}}$

We can note that the length of one side of our square is

so, the one side is equal to

$\begin{gathered} L=2*\frac{8}{\sqrt[]{2}} \\ L=8\sqrt[]{2} \end{gathered}$

Since the area of a square is

the area of our figure is equal to

$\begin{gathered} A=(8\sqrt[]{2})^2 \\ A=64*2 \\ A=128 \end{gathered}$

That is, the area of the square is equal to 128 centimeters squared.