The number of females are F = 553.
The number of persons who oppose the tax is, O = 629.
The total number of person is, T = 1054.
The number of person who are femal and oppose the tax is, (O and P) = 297.
Determine probability for selected person is female or oppose the tax.
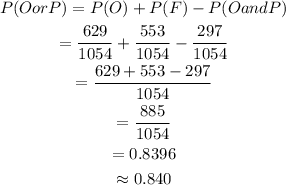
Thus probability for the selected person to be female or oppose the tax is 0.840.
PART (B)
The number of persons are male is M = 501.
The number of person in support of tax is S = 392.
The number of person support the tax and are male is (S and M) = 156.
Determine the probability for selected person supports the tax and is male.

Thus probability for selected person to be men or in support of tax is 0.699.
PART C
The number of person not unsure of tax is N = 1021.
The number of female is F = 553.
The number of person who are femal and not unsure of tax is (N and F) = 533.
Determine the probability for selected person is not unsure or is female is,
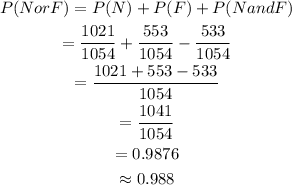
Thus probability for the selected person is not unsure of tax and is female is 0.988.