Question

Solve the following system of equations using an inverse matrix. You must alsoindicate the inverse matrix, A-1, that was used to solve the system. You mayoptionally write the inverse matrix with a scalar coefficient.X-9y = -4- 3+7y = 579A-112y =1

Answer 1

The given system of equations is,

`\begin{gathered} x-9y=-4 \\ -x+7y=5 \end{gathered}`

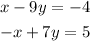
A system of equations can be defined as,

`AX=B\text{ ------(1)}`

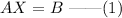
Here, A is the ceofficient matrix, X is the variable matrix and B is the constant matrix.

Coefficient matrix gives the coefficients of the variables in the system of equations. Hence,

`A=\begin{bmatrix}{1} & {-9} & {} \\ {-1} & {7} & {} \\ {} & {} & {}\end{bmatrix}`

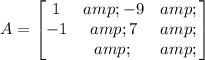
Hence, equation (1) can be written as,

`\begin{bmatrix}{1} & {-9} & {} \\ {-1} & {7} & {} \\ {} & {} & {}\end{bmatrix}\begin{bmatrix}{x} & {} & {} \\ {y} & {} & {} \\ {} & {} & {}\end{bmatrix}=\begin{bmatrix}{-4} & & {} \\ {5} & & {} \\ {} & {} & {}\end{bmatrix}\text{ -------(2)}`

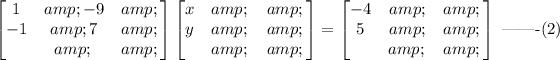
If a 2x2 matrix A is given by,

`A=\begin{bmatrix}{a} & {b} & {} \\ {c} & {d} & \\ {} & {} & {}\end{bmatrix}`

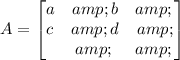
Then, adj A is, Hence, the adjoint of the given matrix A is,

`adjA=\begin{bmatrix}{d} & {-b} & {} \\ {-c} & {a} & \\ {} & {} & {}\end{bmatrix}`

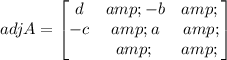
The determinat of A is,

`|A|=ad-bc`

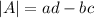
Hence, the inverse of the given matrix A is,

`\begin{gathered} A^(-1)=(1)/(|A|)adj\text{ A} \\ =(1)/(7*1-(-9*(-1)))\begin{bmatrix}{7} & {9} & {} \\ {1} & {1} & {} \\ {} & {} & {}\end{bmatrix} \\ =(1)/(7-9)\begin{bmatrix}{7} & {9} & {} \\ {1} & {1} & {} \\ {} & {} & {}\end{bmatrix} \\ =(1)/(-2)\begin{bmatrix}{7} & {9} & {} \\ {1} & {1} & {} \\ {} & {} & {}\end{bmatrix} \end{gathered}`

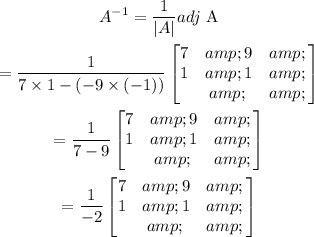
Now, multiply equation (1) by inverse of A to solve for the variable matrix.

Here, I is identity matrix.

Therefore, the inverse of matrix A is,

`A^(-1)=(-1)/(2)\begin{bmatrix}{7} & {9} & {} \\ {1} & {1} & {} \\ {} & {} & {}\end{bmatrix}`

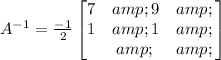
x=-17/2 and y=-1/2.