Question

A toy car with of mass m1 moves in a circular path of radius r on a flat, level table at constant linear speed v. The car is attached to a string that passes through a hole in the middle of the table. A brass ball of mass m2 is attached to the other end of the string and hangs vertically under the table. All frictional forces are considered to be negligible.Which equation correctly shows how the given variables are related? a. m2 = m1*v / r b. m1*g = m2*v*r^2c. m2*g = m1*v^2 / rd. m1*g = m2*v^2 / re. m2*g = m1*v*r^2f. m1 = m2*v / r

Answer 1

Given:

The mass of the car is,

`m_1`

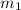
The mass of the brass ball is,

`m_2`

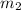
The radius of the circular path is,

`r`

and the constant linear speed of the car is,

`v`

To find:

The correct equation of the variables

Explanation:

As the friction is negligible, the tension at the horizontal string is,

`T=(m_1v^2)/(r)`

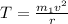
The tension in the vertical string is,

`T=m_2g`

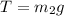
As there is no friction,

`m_2g=(m_1v^2)/(r)`

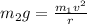
Hence, the correct option is (c).

Answer 2

C

Step-by-step explanation:

Comment

What an interesting question! It is a good one to get to get to know how the answer was derived.

Equation

M2 g is the gravitational force . It's the one that is keeping the toy car going in a circle.

The circular force is F = m1*v^2/r. This force pulls on the string to hold m1 moving a circle.

The key to the question is that both forces have to be equal.

m2*g = m1*v^2/r

Solution

The only answer that works and looks like what I have written is C