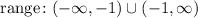Question

Write the equations for all vertical horizontal asymptotes. Vertical asymptote(s):Horizontal asymptote(s):Find all x-intercepts and y-intercept(s):Find the domain and range of f. Write each answer as an interval or union of intervals. Domain:Range:

Answer 1

We have the next graph

And we must find:

1. Vertical asymptote(s):

We can see that there is a vertical asymptote when x = 2.

So, the vertical asymptote is

`x=2`

2. Horizontal asymptote(s):

We can see that there is a horizontal asymptote y = -1

So, the horizontal aymptote is

`y=-1`

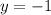
3. x-intercept(s) and y-intercept(s):

We can see the graph intercepts the x-axis when x = -6

So, the x-intercept is (-6, 0)

We can see the graph intercepts the y-axis when y = 3

So, the y-intercept is (0, 3)

4. Domain nd Range:

Domain: The domain is the set of numbers that we can take in x-axis for the function.

Since we have a vertical asymptote that is x = 2 and we don´t have any more vertical asymptote the domain will be all real numbers except the value of the asymptote. So, the domain is

`\text{domain}\colon(-\infty,2)\cup(2,\infty)`

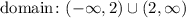
Range: The range is the set of numbers that the function takes in the y-axis.

Since we have only one horizontal asymptote the range will be all reals numbers except the value of the horizontal asymptote. So, the range is

`\text{range}\colon(-\infty,-1)\cup(-1,\infty)`