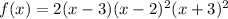we have that
the polynomial is of the form
f(x)=a(x-3)(x-2)^2(x+3)^2
where
a is the leading coefficient
y-intercept -----> (0,-216)
For x=0
substitute and solve for a
-216=a(0-3)(0-2)^2)(0+3)^2
-216=a(-3)(-2)^2(3)^2
-216=a(-3)(4)(9)
-216=-108a
a=2
therefore