we have the functions
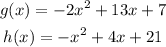
Part A
Equate both equations
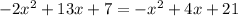
Solve for x
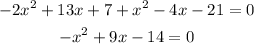
Solve the quadratic equation
using the formula
a=-1
b=9
c=-14
substitute
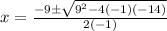
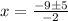
The values of are
x=2 and x=7
The answer Part A
The distances are x=2 units and x=7 units
Part B
f(x)=g(x)/h(x)
so
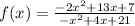
Rewrite in factored form

The given function has a discontinuity at x=7 (hole), a vertical asymptote at x=-3
and horizontal asymptote at y=2