Question

1. Imagine a scatter plot was created based on the data in this table. Which equation best represents the trend line for the data?

X 5,10,15,20,13 Y 4,7,10,13,9

Answer 1

Based on the data in this table, the equation that best represent it is

• y = 3/5 x + 1

How to find the equation of the straight line

The equation of the line is written on the form

y = mx + c

where

m is the slope

c is the y-intercept

the slope, m is calculated using the points on the table (5, 4) and (10, 7)

m = (y₀ - y₁) / (x₀ - x₁)

m = (4 - 7) / (5 - 10)

m = (-3) / (-5)

m = 3/5

Using the point slope form of the equation of a straight line, with points (5, 4)

y - y₀ = m (x - x₀)

y - 4 = 3/5 (x - 5)

y = 3/5 x - 3 + 4

y = 3/5 x + 1

Answer 2

Let us take two points from the table values,

(5,4) and (10,7)

To find the equation:

First, find the slope of th equation

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ =(7-4)/(10-5) \\ =(3)/(5) \end{gathered}`

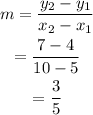
Then, substitute the slope in the slope intercept form of an equation,

`\begin{gathered} y=mx+c \\ y=(3)/(5)x+c\ldots\ldots.(1) \end{gathered}`

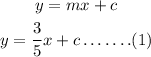
Next, lets find the y-intercept c:

Since, the equation passes through the point (5,4) ,

Hence,

`\begin{gathered} 4=(3)/(5)(5)+c \\ 4=3+c \\ c=1 \end{gathered}`

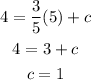
Substitute c=1 in equation (1) we get,

`y=(3)/(5)x+1`

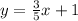
Hence, the correct option is C.