We have the quadratic equation:
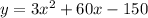
And want to write in the vertex form by completing the square, so we take the coefficient of squared x as a factor:
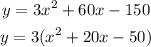
Take the coefficient of x and divided by 2 and the calculate the square, and add and substract the result into the parenthesys, so:

Now, write the parenthesys as a binomial squared:
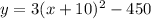
The option a) is the correct answer.