Question

mean difference is t for The Standard deliaftor of a Sample taken from Population A is 17.6 for a Sample of 25. The Standard deviation of a Sample taken from Population B is 21.2 for a sample of 30. The Standard deviation of the Sample mean difference is

Answer 1

Answer:

The standard deviation of a mean difference = 5.23

Step-by-step explanation:

Given:

Standard deviation of a sample taken from population A = 17.6

the number of samples = 25

Standard deviation of a sample taken from population B = 21.1

the number of samples = 30

To find:

the standard deviation of the mean difference

The standard deviation of a mean difference is given as:

`\begin{gathered} \sigma\text{ = }\sqrt{(\sigma_(A^2))/(n_A)+(\sigma_B^2)/(n_B)} \\ \sigma\text{ = standard deviation of the sample mean difference} \end{gathered}`
`\begin{gathered} \sigma\text{ = }\sqrt{(17.6^2)/(25)+(21.2^2)/(30)} \\ \\ \sigma\text{ = }√(12.3904+14.9813) \\ \\ \sigma\text{ = }√(27.3717) \\ \\ \sigma\text{ = 5.23} \end{gathered}`

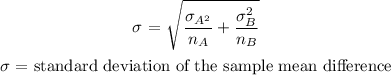
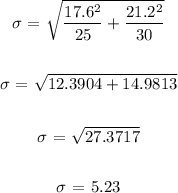
The standard deviation of a mean difference = 5.23