We have three tests of symmetry. In respect to the y-axis or in respect to the x-axis, or in respect to the origin.
For symmetry with respect to the Y-Axis, check to see if the equation is the same when we replace x with −x:

Since the equation remains the same when we change the sign of the x variable, the equation is symmetric in respect to the y-axis.
For symmetry with respect to the X-Axis, check to see if the equation is the same when we replace y with −y:
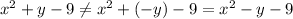
Since the equation does not remains the same when we change the sign of the y variable, the equation is not symmetric in respect to the x-axis.
The equation is symmetric with respect to the origin if for every point (x,y) that satisfies the equation, the point (-x, -y) also satisfies the equation.
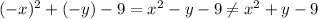
Since it doesn't satisfies this condition, the equation is not symmetric with respect to the origin.